题目描述

小 C 非常喜欢树。上次后院的蚂蚁看腻了，这次准备来观察树。

小 C 每天起得早早的，给小树浇水，并且每天记录这棵小树的一些数据。树在小 C 的精心呵护下不断长大。经过若干天的记录，小 C 竟然发现了一棵树生长的规律！

为了阐述其规律，小 C 想先使用一种严谨的语言来抽象化一棵树。

首先，小 C 用图论的概念定义了一棵树 $T =< V,E >$，$V$ 表示所有点构成的集合，$E$ 表示所有边（无向边）构成的集合。一棵具有一定形态的树用一个大写字母简记，一般会使用 $T$；其大小等于 $|V|$，即节点的个数。

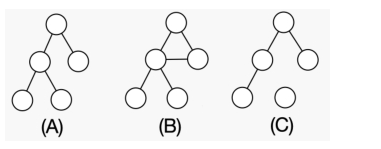
小 C 发现所有树都有一个共同点：大小为 $n$ 的树，恰好含有 $n − 1$ 条边，并且任意两个节点间存在路径使得互相可达。比如说下图中 (A) 是一棵树，而 (B)(C) 却不是。

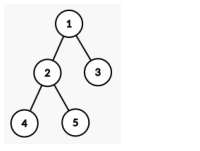
自然界中所有树都有根，对于树 $T$ 也有且仅有一个根，其为 $V$ 中的某个节点 $r$。于是 小 C 可以对所有节点定义深度，节点 $u$ 的深度等于 $u$ 到 $r$ 的距离 $+1$，例如下面这棵树中，令节点 $1$ 为根 $r$，则节点 $2$、$3$ 的深度为 $2$，节点 $4$、$5$ 的深度为 $3$，而节点 $1$ 自身的深度为 $1$。

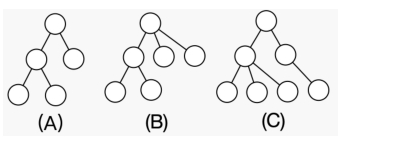
由此可以看出，抽象出来的树和现实中的树正好上下颠倒了。接下来小 C 开始定义生长。某次生长操作用 $T = grow(T’,d)$ 表示，$T’$表示生长前的树，$T$ 表示生长之后的树。 成长规律根据参数 $d$ 决定。生长时，$T’$中所有深度为 $d$ 的节点同时增加一个新的节点与之连接，得到的树即为 $T$。比如说下图中 (A) 为原树 $T$，(B) 为 $grow(T,1)$，(C) 为 $grow(T,2)$。

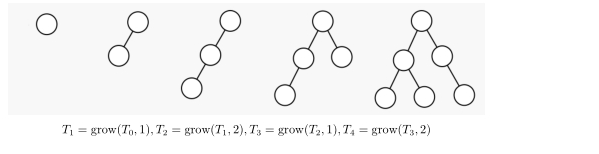
小 C 又定义成长，表示一棵树经过一系列生长得到另一棵树的过程。令原树为 $T_0$， 总共 $k$ 次生长操作，第 $i$ 次生长的参数为 $d_i$ ，则可以表示为：

$$T_1 = grow(T_0 ,d_1 ) → T_2 = grow(T_1 ,d_2 ) → ··· → T_k = grow(T_{k−1} ,d_k ) $$

小 C 又定义种子为大小为 $1$、仅包含根节点的树。下图是一颗种子的成长过程。

然而一个猜想需要诸多事实来支撑。小 C 又观察了许多棵树，然而树儿都长大了，小 C 只能得到成长之后的树 $T$。他想知道对于一颗种子，存不存在某种成长过程，使得种子 能长成树 $T$。于是小 C 把问题交给了你。

本题每个输入文件有多组测试数据

输入格式

从文件 observe.in 中读取数据。 第一行一个正整数 $Q$，表示数据组数。

对于每组数据，将会描述一棵成长之后的树 $T$；

每组数第一行两个正整数 $n$ 和 $r$，表示树 $T$ 的大小、$T$ 的根，节点依次从 $1$ 到 $n$ 标号；

接下来 $n − 1$ 行，每行两个整数 $u$ 和 $v$，描述一条边 $(u,v)$。

保证 $T$ 一定是一棵合法的树。

输出格式

输出到文件 observe.out 中。 总共 $Q$ 行，每行表示对应的树 $T$ 是否存在成长过程，使得种子成长成 $T$，如果存在， 输出 Yes，否则输出 No（请注意大小写）。

样例

1
6 1
1 2
1 3
2 4
2 5
3 6

Yes

解释#1

这棵树的形态如下。

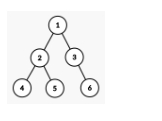
此为题面描述的成长过程中的例子。

1
6 1
1 2
2 3
3 4
1 5
5 6

No

解释#2

这棵树的形态如下。

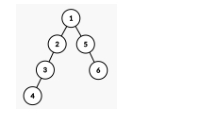
一颗种子不存在某种成长方式变成这棵树。

2
6 1
1 2
1 3
2 4
2 5
3 6
6 1
1 2
2 3
3 4
1 5
5 6

Yes
No

样例4-5

请下载附件查看（附件）。

数据范围

• 对于 $10\%$ 的数据：$n≤5$。
• 对于 $30\%$ 的数据：$n≤10$。
• 对于 $50\%$ 的数据：$n≤100$。
• 对于 $70\%$ 的数据：$n≤3×10^3$。
• 对于 $100\%$ 的数据：$1 ≤ Q ≤ 10$，$1 ≤ n ≤ 10^5$，$1 ≤ r ≤ n$。